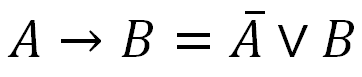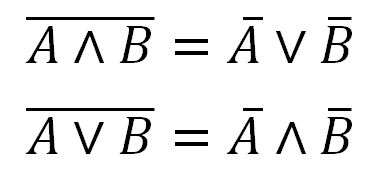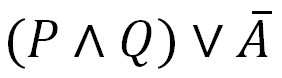А10 ЕГЭ по информатике

Продолжаем подготовку к ЕГЭ по информатике и сегодня рассмотрим решение задач типа A10.

Задачи этого типа довольно сложны. Подходить к их решению, не зная основ логики не стоит. Поэтому настоятельно рекомендую прочитать про конъюнкцию, дизъюнкцию, импликацию.

Давайте начнем рассмотрение с решения задачи А10 ЕГЭ 2014 по информатике из демоверсии с сайта ФИПИ.

На числовой прямой даны два отрезка: P = [1, 39] и Q = [23, 58].
Выберите из предложенных отрезков такой отрезок A, что логическое выражение
( (x ∈ P) → ¬ (x ∈ Q) )→ ¬ (x ∈ А)
тождественно истинно, то есть принимает значение 1 при любом значении переменной х.
1) [5, 20]       2) [25, 35]       3) [40, 55]       4) [20, 40]

Решение:

Для удобства давайте обозначим наши простые высказывания большими латинскими буквами (по названию отрезков):

• P: x ∈ P
• Q: x ∈ Q
• A: x ∈ А

Перепишем наше выражение в более удобном виде:

Задача 10 ЕГЭ по информатике

Теперь небольшое отступление про импликацию. Импликацию можно выразить через дизъюнкцию и отрицание вот таким образом:

Раскрытие импликации через дизъюнкцию и отрицание

Это очень важное правило и его необходимо запомнить.

Теперь мы можем переписать наше высказывание, уйдя от импликации:

Преобразование высказывания

Чтобы упростить выражение в скобках воспользуемся законом де Моргана (второй на картинке)

Законы де Моргана

В итоге получим

Преобразуем высказывание

Применив закон двойного отрицания получим итоговое высказывание с котором и будем работать дальше. Да, это еще не все :)

Итоговое высказывание

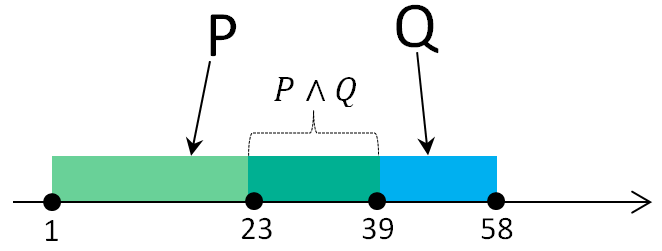
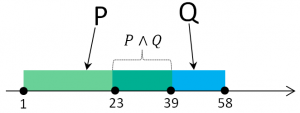
Теперь давайте вспомним, что наши высказывания — это отрезки и отобразим их на координатной прямой.

График для задачи

Проанализируем график и итоговое высказывание. Итоговое высказывание должно быть истинным при любом значении х по условию задачи. В итоговом высказывании у нас выражение в скобках и инверсия A соединены дизъюнкцией. Дизъюнкция истинна когда хотя бы одно или оба высказывания истинны. Значит итоговое высказывание будет истинным когда либо выражение в скобках истинно, либо отрицание A истинно, либо истинны оба выражения (в скобках и отрицание A). Выражение в скобках — конъюнкция, а она истинна только когда оба высказывания истинны. Т. е. когда x принадлежит промежутку [23, 39] итоговое высказывание будет истинным. В противном случае высказывание будет ложным и тогда отрицание A должно быть истинным. Раcсмотрим, когда оно таким будет.

В начале мы определились, что высказывание A означает, что x ∈ А. Так как оно у нас с отрицанием, то отрицание A будет означать, что x ∉ A, а значит точка x должна принадлежать диапазону [-∞, 23] или [39, +∞]. Осталось найти такой отрезок A, который будет перекрывать диапазон [23, 39] (так как у нас он с отрицанием, то в итоге получится нужный нам диапазон). Т. е. левая координата отрезка должна быть больше или равна 23, а правая меньше или равна 39.

Из предложенных вариантов подходит только [25, 35]. Правильный ответ — 2.

Еще один пример решения задачи A10 ЕГЭ по информатике (по просьбе Евгении):

На числовой прямой даны три отрезка:

P = [0,40], Q=[20,45] и R=[10,50].

Выберите такой отрезок A, что формула ((x∈P) → (x∈Q)) ∨ ((x∉A) → (x∉R)) тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [5,20]       2) [10,15]       3) [15,20]       4) [35,50]

Решение:

Для удобства примем следующие обозначения:

P: x∈P

Q: x∈Q

A: x∈A

R: x∈R

Теперь нашу формулу мы сможем переписать в таком виде:

(P → Q) ∨ (¬A → ¬R)

 Применив закон де Моргана, получим следующее:

(¬P ∨ Q) ∨ (A ∨ ¬R)

Для удобства обозначим выражения в скобках так:

Y = ¬P ∨ Q

Z = A ∨ ¬R

Осталось отобразить формулу на числовой прямой.

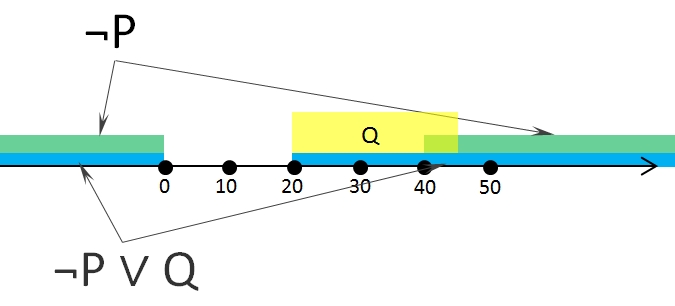
Рассмотрим выражение Z и перенесем его на числовую прямую

A10 ЕГЭ 2014 по информатике

Здесь у нас зеленым цветом обозначена область ¬P, желтым — Q, а голубым — область ¬P ∨ Q.

Теперь заметим, что выражения в скобках объединены дизъюнкцией, а это значит, что итоговое выражение будет тождественно истинным когда хотя бы одно или оба сразу выражения в скобках истинны.

Сейчас мы видим, что если переменная х принадлежит диапазону [-∞;0] или [40; +∞], то итоговое выражение будет истинно.

Рассмотрим второе выражение A ∨ ¬R (я удалил на предыдущем рисунке области ¬P и Q, чтоб они не мешали, оставив только конечную область ¬P ∨ Q):

Решение задачи A10 ЕГЭ по информатике

Как видим, выражение во второй скобке будет истинно только когда x принадлежит диапазону [-∞;10] или [50; +∞].  Общее выражение будет истинно когда x принадлежит диапазону [-∞;10] или [20; +∞].

А вот если x находится в диапазоне (10; 20), то итоговое выражение будет ложным. Значит нам надо найти такое значение диапазона A, которое перекроет диапазон (10; 20). Из предложенных в условии вариантов этому условию удовлетворяет только диапазон [5,20].

Правильный ответ: 1.

Я понимаю, что задачи типа A10 ЕГЭ по информатике — это довольно сложное задание, хотя и относится к части A. Поэтому всегда рад ответить на ваши вопросы в комментариях.