Решение задачи 4 ЕГЭ (ГВЭ) по информатике
Для решения подобных задач необходимо умение переводить числа из десятичной системы счисления в двоичную. Это можно сделать вручную или воспользоваться сервисом на нашем сайте.
Текст задачи 4 ЕГЭ (ГВЭ) по информатике 2015 из демоверсии ФИПИ:
Решение:
Для решения необходимо перевести 519 в двоичную систему счисления и посчитать количество единиц. Выглядит это таким образом:

Решение задачи 4 ЕГЭ (ГВЭ) по информатике
Как видим, количество единиц в результате 4. Это и есть правильный ответ.
Решение (2 способ):
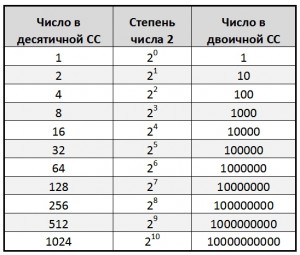
Данный способ заключается в следующем. Давайте посмотрим на степени числа 2 в десятичной и двоичной системе счисления:
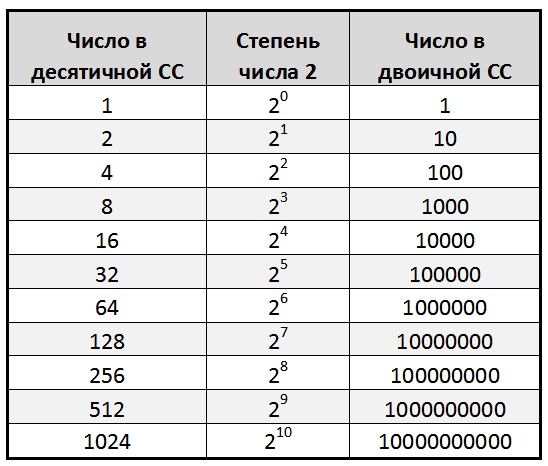
Степени числа 2
Заметьте, что 2 в любой степени в двоичной системе счисления всегда содержит только одну единицу! Зная это, давайте попробуем разложить число 519 на степени двойки:
519 = 512 + 7 = 29 + 7 = 29 + 4 + 3 = 29 + 22 + 3 = 29 + 22 + 2 + 1 = 29 + 22 + 21 + 1
Каждое из слагаемых содержит одну единицу. А так как они находятся в разных разрядах, то можно смело утверждать, что количество единиц в числе будет равно количеству слагаемых, т. е. в нашем случае 4.
Ответ — 4.
Автор: Александр Чернышов

3 комментария
Доходчиво и понятно. Но если число 510 десятичная сс то сколько единиц в двоичной сс? 2(9)степени= 512 минус 2(1)спепени можно ли узнать колличество единиц так. Минусовать степени результат превратить в колличесво едениц??? 9-1=8 восемь значащих единиц
Да, без деления на двойку определить количество единиц гораздо проще. да и полезнее знать степени двойки и применять.
510 — первая меньшая чем 510 степень двойки это 2^8,
далее последовательно вычитаем
519-512=7
7-4=3
3-2=1
1-1=0
нашли 4 степени двойки в этом числе (512,4,2,1). значит и единиц в числе 519 четыре.
вначале опечатка,
строку 510 — первая меньшая чем 510 степень двойки это 2^8,
надо читать так:
для 519 — первая меньшая чем 519 степень двойки это 2^9 = 512