Решение задач типа 11 ГИА по информатике

Сегодня мы рассмотрим решение задачи 11 ГИА по информатике. Для примера возьмем задачу 2014 года из демоверсии ФИПИ.На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
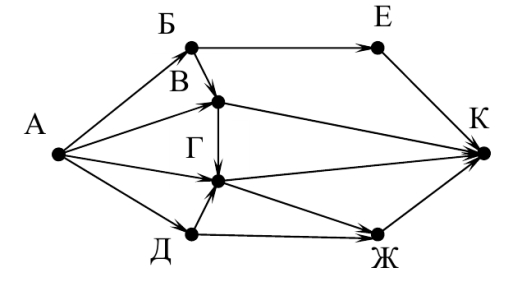
Решение задач типа 11 ГИА по информатике
Данный тип задач нацелен на проверку умения анализировать информацию, представленную в виде схем. При решении есть вероятность запутаться в большом количестве вариантов.
По опыту могу сказать, что мои ученики справляются с подобными задачами методом перебора. Но мы рассмотрим другой способ, который можно использовать для подстраховки.
Итак, начнем решение с конца, т. е. с города К. Как мы видим, в город К можно приехать из городов Е, В, Г, Ж. Отобразим это графически
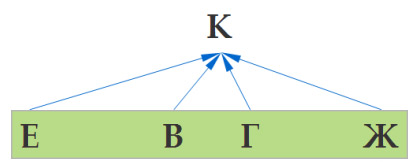
Задача 11 ГИА по информатике. Шаг 1
Далее, на втором шаге определим, откуда можно добраться в города Е, В, Г, Ж. К примеру,
- в город Е можно добраться только из города Б,
- в город В — из городов А и Б,
- в город Г из городов А, В и Д,
- в город Ж из городов Г и Д.
Графически это будет выглядеть таким образом:

Задача 11 ГИА по информатике. Шаг 2
Таким образом, мы будем продолжать до тех пор, пока каждая ветка не приведет к городу А. В итоге получится такая диаграмма — дерево:
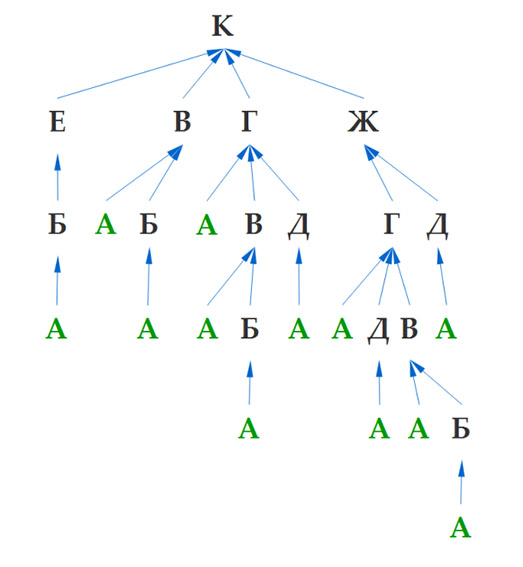
Задача 11 ГИА по информатике. Шаг 3
Здесь зеленым цветом я выделил конечные пункты — город А. Осталось только посчитать их количество — это и будет правильный ответ. В нашем случае их 12. Правильный ответ: 12.
Автор: Александр Чернышов

3 комментария
решение: из а через б 4 дороги;
из а через в 3 дороги;
из а через г 2 дороги;
из а через д 3 дороги: суммируем 4+3+2+3=12 путей из а в к
Проще решать с конца (почти так как и показано, только не строить все пути). Даем вершине К значение 1 (т.к. дорог из К в К одна). Считаются значения всех вершин, дуги из которых выходят только в пункт К (Е = К = 1, Ж = К = 1). Затем считается значения вершин, дуги из которых выходят только в определенные ранее (Г = К + Ж = 1 + 1 = 2). Повторяем по тех пор, пока не достигнем решения. 2 шаг — Д = Г + Ж = 2 + 1 = 3, В = К + Г = 1 + 2 = 3. 3 шаг — Б = В + Е = 3 + 1 = 4. 4 шаг — А = Б + В + Г + Д = 4 + 3 + 2 + 3 = 12.
Итого ответ 12.
Круто очень, всё понятно!